八大算法
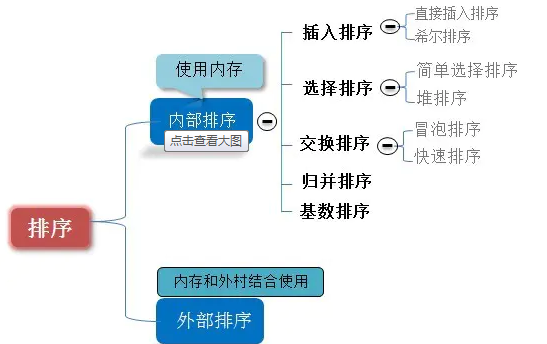
- 见链接https://juejin.im/post/5ab9ae9cf265da23830ae617
- https://juejin.im/post/58c9d5fb1b69e6006b686bce#heading-14
排序
1. 时间复杂度
时间复杂度来表示执行的次数,,树容量N有关,下面详细讲解基本排序的时间复杂度
1.1 冒泡排序
思路
- 最外层遍历将最大的元素放在最后
- 内层遍历前面的最值
1 | function swap(arr, i, j) { |
- 时间复杂度的分析O(n^2)
- 空间:O(1)
- 稳定
1.2 选择排序
思路
每次都从后面元素中选出最值存放在前面,依次类推,两层循环嵌套
时间复杂度==O(n^2)
1 | //2.选择排序 |
- 时间复杂度:O(N^2)
- 空间复杂度:O(1)
- 不稳定
1.3 插入排序
思路
插入排序 :从第一位开始排序,始终保证前面的元素是排好序的,每次从后面未排的元素中依次取出元素和拍好序的元素进行对比并插入到排好序的元素中
插入排序和数组是否有序有直接关系
时间复杂度
- 插入排序和是否有序有关
- 有序:O(n)
- 逆序:N*交换次数N=O(n^2)
- 时间复杂度以最坏情况下为基础
- 不稳定
1 | // 3.插入排序 |
1.4 排序的对数器
- test函数
- testTime:测试次数
- size:数组的长度
- value:数值范围
- sortType:排序算法的类型
1 | const { bubbleSort, InsertSort, selectSort } = require('./01_sort') |
递归
1 时间复杂度
1.1 递归通用的时间复杂度分析(Master定理)

- a:表示一共这个过程发生了多少次,就看代码中发生的次数(也就是递归调用的次数),不用看执行的次数
- N/b:子样本量
- T(N/b):子样本量的时间复杂度
- O(N^d):除去子过程调用之外,剩下过程的时间复杂度是多少
master公式的使用范围:划分子过程的规模是一样的,也就是每次b的值是一样,只是发生的次数a不一样
2 复杂度练习
2.1 递归求解数组中的最大
思路
- 先求解左边的最大值,
- 在求解右边的最大值
- 在求左右两边的最大值
- 递归结束的条件是:start==end
代码
1 | //通过递归实现求解最大值 |
时间复杂度分析(满足master)
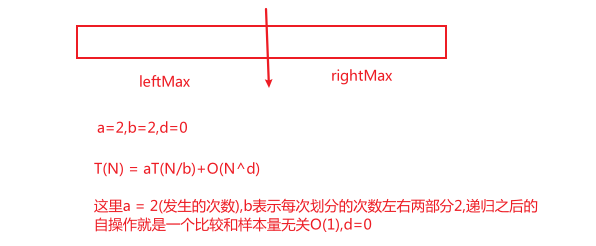
logb(a)=log2(2)=1>0,所以O(N^(logb(a)))=O(N)
2.2 归并排序(采用的是分治的思想)
分析
- 第一,归并排序是原地排序算法吗 ? 这是因为归并排序的合并函数,在合并两个有序数组为一个有序数组时,需要借助额外的存储空间。实际上,尽管每次合并操作都需要申请额外的内存空间,但在合并完成之后,临时开辟的内存空间就被释放掉了。在任意时刻,CPU 只会有一个函数在执行,也就只会有一个临时的内存空间在使用。临时内存空间最大也不会超过 n 个数据的大小,所以空间复杂度是 O(n)。所以,归并排序不是原地排序算法。
- 第二,归并排序是稳定的排序算法吗 ? merge 方法里面的 left[0] <= right[0] ,保证了值相同的元素,在合并前后的先后顺序不变。归并排序是一种稳定的排序方法。
- 第三,归并排序的时间复杂度是多少 ? 从效率上看,归并排序可算是排序算法中的
佼佼者。假设数组长度为 n,那么拆分数组共需 logn 步, 又每步都是一个普通的合并子数组的过程,时间复杂度为 O(n),故其综合时间复杂度为 O(nlogn)。 最佳情况:T(n) = O(nlogn)。 最差情况:T(n) = O(nlogn)。 平均情况:T(n) = O(nlogn)。
思路
先数组划分为两部分
左右两侧排好序
通过外排,增加临时存储数组temp
添加指针分别指向有序的两部分数组,从头到尾依次比较,谁小谁将值存储在temp中并一定指针,直到有一个先到数组结尾,归并结束
判断两个数组是否同时到达数组结尾,没有直接将后面的元素直接添加到temp中,归并排序结束

分析时间复杂度
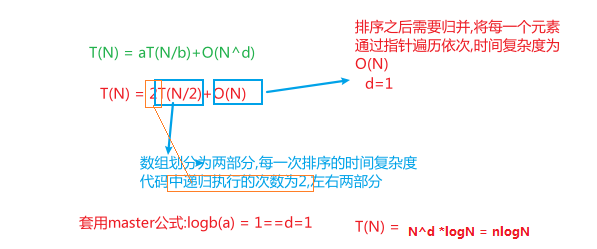
空间复杂度
- 占用了arr数组长度,O(N)
代码
1 | function mergeSort(arr) { |
2.3 小和问题(归并排序的思想来解决)
- 在一个数组中,每个数左边比当前数小的数累加起来,叫做这个数组的小和,求一个数组的小和
思路
(1)直接遍历,时间复杂度为O(N^2)
(2)通过归并排序
分析
[1,3,4,2,5]
1:左边比1小的数:没有
3:左边比3小的数:1
4…..:1,3,
2,…..: 1
5…..:1,3,4
小和=1+1+3++1+1+3+4=16
- 在归并的过程中,如果左边比右边的小,产生小和,(右边的当前指向到末尾有几个值就有左边所指位置的值*指的个数个小和)
问题的转换:求当前位置的值左边比他自身小的值====求当前值右边比他大的值
注意归并排序是没有返回值的,小和问题和逆序问题只是在归并的基础了多了求和问题和返回值问题
1 | //这里借助归并排序来解决小和问题 |
2.4 逆序问题(归并排序思想解决)
题目
求数组中存在的逆序对,这里和小数和正好相反(只需修改左边的数比右边的数大,改变指针的走向,将大数归并)
思路
(1) 遍历,事件复杂度:O(N^2)
(2)归并排序的时间复杂度:nlogn
归并排序快的原因是:去除了重复的操作,在归并的过程中
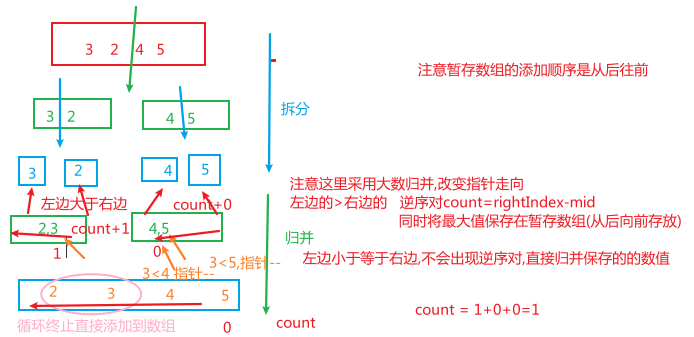
代码
1 |
|
快排
1 数组划分(partion)
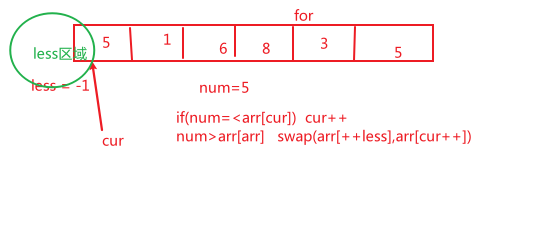
1.1 大于num的放右边,小于放左边(划分为两部分)
思路
本题主要考察的是指针和交换问题
设置小于部分的区域为less,less初始值=-1
当当前值大于num,cur++
小于num和less的下一个值交换,less++,扩大less的范围
注意:这里不考虑是否有序的问题
复杂度
- 时间:O(N)
- 空间:O(1)
代码
1 | function swap(arr, i, j) { |
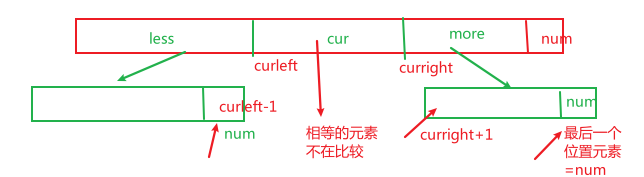
1.2 荷兰国旗问题(划分为3部分)
题目
将数组划分为3部分,大于,等于,和小于

思路
设置三个指针,分别指向左边区域less,右边区域more和当前区域cur
当cur>num arr[–more]和arr[cur]交换位置,当前位置不变继续比较
cur<num arr[++less]和arr[cur++]交换位置,当前位置++
cur = num cur++
结束条件是cur==more
注意:less和more始终指向的less区域和more区域的边界,++less到–more之间的值都是等于num的区间范围,依然不考虑是否有序的问题
复杂度
- 时间:O(N)
- 空间:O(1)
代码
1 | function swap(arr, i, j) { |
2 随机快排
2.1 递归实现(增加了递归的partition问题)
思路
- 快排可以看做在和荷兰问题的基础上不断递归左右已经划分好的子数组,最终返回排序好的数组
- 这里可以进行优化,在递归的过程中不在重复计算已经等于num的数值
- 快排每次将数组的最后的一个数看成基础的base=num来进行荷兰问题递归
复杂度
- 时间:nlogn
- 空间:O(logn),只需执行过程中保存的断点的个数(划分的次数)需要额外的空间存储,断点组成是一个树,logN
- 注意:快速排序有序归并排序,好在快排的常数项小,空间复杂度小
- 这里的时间复杂度和空间复杂度都是一个长期期望
问题分析(数据状况不可控)
- 经典快排和数组是否有序是有关系的,当你每次选择的base不是正中间的数的时候此时划分的左右规模是不相等,当有序的情况下会演变成o(n^2)
- 代码:
swap(arr, parseInt(Math.random() * (R - L + 1)) + L, R)

数据状况不可控的解决方案(绕过原始的数据状况):
- 通过随机的方式打乱数据状况:比如在快排中通过随机选择一个值作为base,就和原始的数据状况没有关系了
- 数据状况通过哈希函数打乱
快排相关知识
- 快排是原地排序算法(不需要额外的空间)
- 快排不稳定(相同的元素可能会调换位置)
代码
1 | function swap(arr, i, j) { |
2.2 非递归实现
3.快排和归并的比较
相同点
- 快排和归并用的都是分治思想,递推公式和递归代码也非常相似
不同点
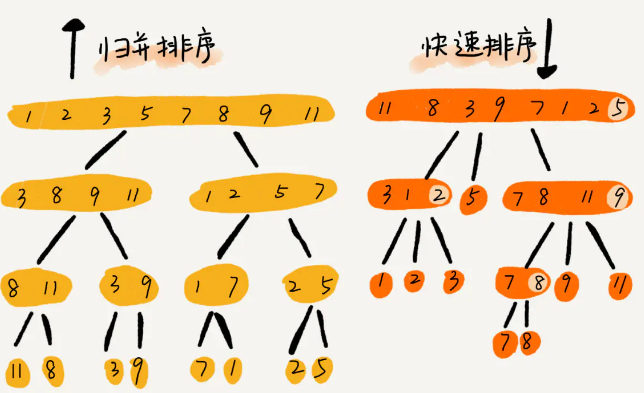
归并排序的处理过程是
由下而上的,先处理子问题,然后再合并。而快排正好相反,它的处理过程是
由上而下的,先分区,然后再处理子问题。归并排序虽然是稳定的、时间复杂度为 O(nlogn) 的排序算法,但是它是非原地排序算法。
归并之所以是非原地排序算法,主要原因是合并函数无法在原地执行。
快速排序通过设计巧妙的原地分区函数,可以实现原地排序,解决了归并排序占用太多内存的问题。
堆
1.1 堆知识点
堆:将数组看成是一个完全二叉树,堆分为大顶堆和小顶堆.
父子元素之间的关系
父元素:(i-1)/2
左孩子:2i+1<n
右还在:2i-1<n,
这里的i是数组的下标值,当他们小于最后数组的长度表示子节点存在没有越界
堆结构非常重要
- 堆结构的插入heapInsert和调整heapify
- 堆结构的增大和减小
- 建立堆的过程,时间复杂度为O(N)
- 优先级队列结构就是堆结构
1.2 堆排序
思路
- 通过遍历,边插入边调整堆
- 交换堆的最大值和最后一个元素,将调整范围-1,调整堆,
- 每次将最大值放在数组的末尾,直到调整范围变为0,此时数组中所有的元素都有序
复杂度
- 时间:O(nlogn)
- 空间:O(1)
- 不稳定
注意
堆在调整的过程中的时间复杂度就是logN,在不断的调整二叉树结构;插入N
通过堆就可以实现一个优先级队列,面试中都是这么实现的
示意图
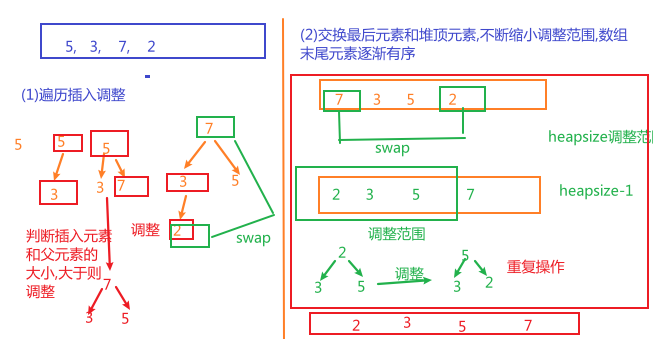
代码
1 | //数组交换 |
其他排序
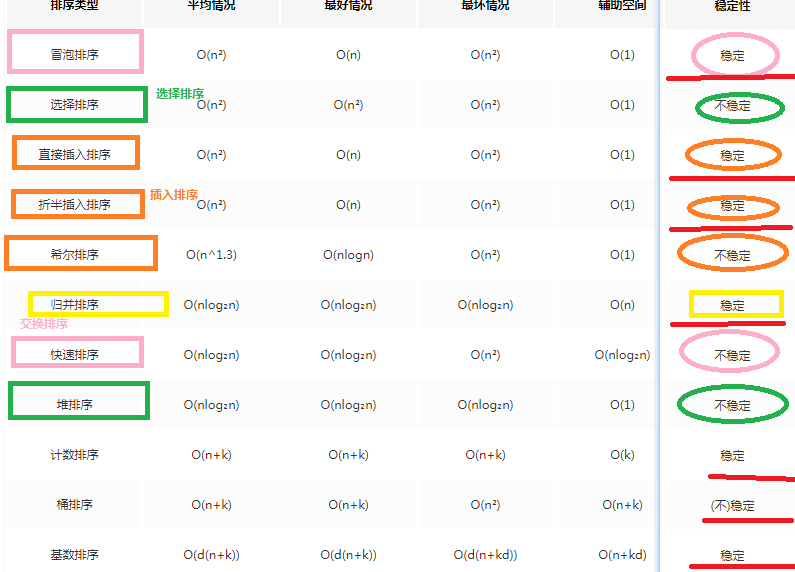
1.1 其他排序
1.2 排序对比
- 见链接https://juejin.im/post/5ab9ae9cf265da23830ae617
- https://juejin.im/post/58c9d5fb1b69e6006b686bce#heading-14

本文链接: https://sparkparis.github.io/2020/06/20/%E7%AE%97%E6%B3%952/
版权声明: 本作品采用 知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议 进行许可。转载请注明出处!


